Department
of Chemical Engineering and Materials Science University of California Davis
Drying Water and Ethanol through a Porous Medium!
By
Brett Koehn
For
Professors Powell and Tseregounis
ECH 155: Chemical Engineering Laboratory
Group #1
Ethan
Jensen, Chris Gee, and Zheyu Li
Experiment Performed: January 29, 2016
Report Submitted: February 9, 2016
TABLE
OF CONTENTS:
Abstract……………………………………………………………………………………………3
Introduction………………………………………………………………………………………..3
Theory……………………………………………………………………………………………..5
Experimental
Methods…………………………………………………………………….………7
Figure
1……………………………………………………………………………………8
Results…………………………………………………………………………………………......9
Figure
2…………………………………………………………………………………..11
Figure3………………………………………………………………………………...…11
Discussion……………………………………………………………………………………..…12
Conclusion…………………………………………………………………………………….…14
Nomenclature
Table……………………………………………………………………………...14
References………………………………………………………………………………………..15
Appendix A………………………………………………………………………………………16
Figure
4…………………………………………………………………………………..16
Figure
5…………………………………………………………………………………..17
Figure
6…………………………………………………………………………………..18
Figure
7…………………………………………………………………………………..19
Figure
8…………………………………………………………………………………..20
Figure
9…………………………………………………………………………………..21
Figure
10…………………………………………………………………………………22
Figure
11………………………………………………………………………………....23
Figure
12………………………………………………………………………………....24
Figure
13………………………………………………………………………………....25
Figure
14………………………………………………………………………………....26
Figure
15………………………………………………………………………………....27
Figure
16………………………………………………………………………………....28
Table
1……………………………………………………………………………….......28
Table
2……………………………………………………………………………….......29
Table
3……………………………………………………………………………….......29
Table
4……………………………………………………………………………….......37
Table
5……………………………………………………………………………….......52
Table
6……………………………………………………………………………….......52
Table
7……………………………………………………………………………….......53
Table
8……………………………………………………………………………….......55
Table
9……………………………………………………………………………….......56
Table
10……………………………………………………………………………….....57
Table
11……………………………………………………………………………….....58
Table
12……………………………………………………………………………….....59
Table
13……………………………………………………………………………….....60
Table
14……………………………………………………………………………….....61
Table
15……………………………………………………………………………….....62
Table
16……………………………………………………………………………….....63
Table
17……………………………………………………………………………….....66
Table
19……………………………………………………………………………….....67
Table
20……………………………………………………………………………….....68
Table
21……………………………………………………………………………….....69
Table
22……………………………………………………………………………….....70
Table
23……………………………………………………………………………….....71
Table
24……………………………………………………………………………….....72
Table
25……………………………………………………………………………….....73
Table
26……………………………………………………………………………….....75
Table
27……………………………………………………………………………….....76
Table
28……………………………………………………………………………….....78
Appendix B………………………………………………………………………………............80
Figure
17………………………………………………………………………………....80
Figure
18………………………………………………………………………………....81
Appendix C………………………………………………………………………………............82
Figure
19………………………………………………………………………………....82
Abstract:
This experiment analyzed how the drying of a liquid is
affected by a porous media. Drying in a porous media has four periods which can
be analyzed: The start-up, constant rate, first falling rate, and second
falling rate periods. In order to analyze these periods, we filled up trays of
ethanol and water, and then dried them and measured the loss in mass versus
time. Next we plotted the loss in mass versus time to find a drying rate.
We
then used the mass versus time plot along with an average saturation versus
drying rate plot to find the constant rate periods. We found constant rate
periods for every trial. The drying rate in the constant rate period was used
to find the heat transfer coefficients. The h values were 26.3±3.4, 34.4±4.5,
23.2±3.0, 48.5±6.3, 38.9±5.1, 20.5±2.7, and 8.1±1.1 watts per meters squared
per degree Kelvin, and the htheory
values were 20.4±.61, 20.9±.62, 19.8±.59, 20.9±.63, 20.8±.62, 19.7±.59,
18.9±.57 watts per meters squared per degree Kelvin.
We
also used a plot of loss in mass versus the square root of time to find the
second falling rate. The Keff and Deff values from the second falling rate period were .018±8.2E5 and
.0436±.009 watts per meters per degree Kelvin and .00014±2.6E6 and .000013±3.9E6 centimeters squared per second
respectively. We found that very small beads must be used to examine
the second falling rate.
Introduction:
The
process of drying involves the dynamics of heat and mass transfer. These two
dynamics happen simultaneously during drying. Also, the phases of liquid and
gas are always involved. For special cases, the solid phase can also be involved.
For example, consider a bowl of vegetable soup being heated in a microwave. The
rate at which liquid evaporates from the bowl will be dependent on the solid
vegetables, the soup broth, and the vapor particles above the soup. Drying
dynamics can be studied by analyzing the corresponding phases involved.
Drying undergoes four different periods which are, in
chronological order, the start-up, constant rate, first falling rate and second
falling rate periods. These periods may be seen in the results section where
average saturation is plotted against drying rate. The start-up period is when
the gas-liquid interface and uniform dryer temperatures are reaching
equilibrium. The constant rate period is when the liquid is still above the
porous medium of beads, and therefore drying is controlled by external heat and
mass transfer. The first period falling rate occurs when the partial of
pressure of the liquid is not equal to the vapor pressure at the gas-liquid
interface. This period happens quickly. The second falling rate period is when
the liquid level is so low that the dried vapor must travel through the dry
porous medium.
Drying is an important aspect of many of industrial
processes. In the pharmaceutical industry several different types of dryers are
used to remove moistures or impurities from pure powders.
The
food and dairy industries are dependent on freeze drying, which is a process
that removes or dries the ice of a product that is frozen rapidly.
Understanding
the dynamics of drying allows industries to maximize the efficiency of their
drying processes. According to Carranza, drying can be maximized by using dry
air to influence the concentration gradient across the gas-liquid interface.
Drying will be the quickest if the gas at the liquid-gas interface is
constantly being renewed.
Theory:
Drying through a
porous medium is dependent largely on the two parameters porosity and
saturation. Porosity is
where ε is porosity, Vγ is the volume of the gas in milliliters, Vβ is the volume of the
liquid in milliliters, and VT
is total volume of the tray in milliliters. Saturation is
where S is the average
saturation.
The
complex dynamics of drying behave specifically during the four periods. The
start-up periods, and first falling rate periods are too complex to analyze
quantitatively. Therefore, we only analyzed them qualitatively. The start-up
period is assumed to quasi-steady state. Also, the temperature of the wet
porous medium, Ta is assumed to be less than the drier temperature,  . Furthermore, we assumed that the
gas-liquid interface or simply interfacial temperature, Ti, is equal
to the wet-bulb temperature, which is less than Ta.
. Furthermore, we assumed that the
gas-liquid interface or simply interfacial temperature, Ti, is equal
to the wet-bulb temperature, which is less than Ta.
We
assumed that the constant rate period obeys the equation
because the fluid
evaporates from the wet porous media since the drier is at a higher temperature
than the wet porous media. H is the
heat transfer coefficient in watts per meters squared per degree Kelvin Δhvap is the liquid heat of
vaporization in joules per mole, A is
the area of the gas-liquid interface in meters squared, and dm/dt is the mass drying rate of liquid
in grams per second. The theoretical heat transfer coefficient can be found
through boundary layer analysis,
where kair is the thermal
conductivity of air in watts per meter Kelvin, L is the height of the tray in meters,  is the width of the insulation in meters, Npr is the Prandtl number,
and NRe is the Reynolds
number which is defined as
is the width of the insulation in meters, Npr is the Prandtl number,
and NRe is the Reynolds
number which is defined as
where u is the velocity of flowing air in meters per
second, DH is the
hydraulic diameter in meters, and ν
is the kinematic viscosity of air in meters squared per second.
The Nusselt number is
where
NNu is the nusselt number, havg is the heat transfer coefficient average over the
gas-liquid interface, L is the same
as DH.
The second falling rate has heat
transfer defined by
where
Z is the height of glass beads in the
tray in meters, z(t) is the height of
the liquid level in meters, and Keff
is the effective thermal conductivity in watts per meter per degree Kelvin.
We also know that diffusive
transport dominates diffusive transport because of the quasi-steady state
assumption. Therefore,
where
Naz is the average molar flux
of vapor in moles per meters squared per seconds, c is the liquid concentration in moles per meters cubed, Xea is the mole fraction of evaporated liquid at gas-liquid
interface, Xa is the mole fraction of liquid in the air above the tray, Deff is the effective
diffusivity, and MWA is
the molecular weight of the liquid.
The dry and wet bulb relationship is
described by Bird’s Transport Phenomena
as
where Nsc is the Schmidt number Cpf is the heat
capacity of air, Pavap is the vapor
pressure of liquid, P is the
pressure inside the dryer, and Twb is the
temperature of the wet bulb.
The theoretical
calculation of the diffusivity is
where Dtheory
is diffusivity of water or ethanol in the porous medium in centimeters squared
per seconds, DAB is the
standard diffusivity of water or ethanol.
Experimental Methods:
We began this experiment by coming
in on Thursday January 28, 2016 to prepare a dish containing glass beads and
water. We measured the mass and volume of the tray, the mass of beads, and mass
of liquid. We converted the masses of liquids and beads to volumes. We then
calculated the porosity. This dish had a large diameter and small height.
Furthermore, this dish was suspended in the dryer. This dish was dried
overnight, and a remote computer recorded the data. We set dryer to an air flow
of 3 and let this dish dry overnight.
Figure 1: The drying duct we
used for this experiment. The knobs on the side adjust the airflow and
temperature (the temperature knob was broken). The glass window is where the
water and ethanol sample were inserted and removed.
The following day, we again
calculated the porosity of trays filled with glass beads and liquids by the
same method described in the paragraph above. However, for liquid we used both
water and ethanol. We ran two trials for water, and four trials for ethanol.
For the water trials we used 4 millimeter and 500 micron beads, and these
trials will be referred to as trials 1 and 2 respectively. For the ethanol
trials we used 4 millimeter, 500 micron, 1 millimeter, and 6 millimeters beads,
and these trials will be referred to as trials 3, 4, 5, and 6 respectively. We
wanted to choose a vast array of bead sizes so we would get varying
diffusivities and heat transfer coefficients. The overnight water trial will be
referred to as trial 7. We measured the mass every 10 minutes and 5 minutes for
water and ethanol trials respectively. We removed the trays and weighed them on
a balance, then another group member would record the data in excel. We also
measured the wet and dry bulb temperatures every hour.
We then plotted the mass versus time
and the change in mass over the change in time versus saturation. We then
searched the mass versus time plots (figure 2, 4, 6, 9, 11, 13, and
15) to find a linear fit. We also searched the change in mass over
the change in time versus average saturation plots (figure 3,
5, 7, 10, 12, 14, and 16) to find a flat period.
Using this information we found in these two plots together, we estimated where
the constant rate period was. We then fit this period linearly on the mass
versus time plot to obtain a dm/dt value for the constant rate period. We then
used this fit to find in accordance with equation 3 to find the experimental
heat transfer coefficient h, which is
shown in appendix B. We also found htheory
by performing a boundary layer analysis and solving equation 4, which is also
shown in appendix B. In equation 4 the Reynolds number was calculated inside
the duct, and we looked up the Prandtl number.
We then plotted the mass versus the
square root time. We then examined this plot and the average saturation plot to
estimate the second falling rate. We then linearly fitted the second falling
rate period to obtain another dm/dt value. We then were able calculate Keff from equation 7, which
is shown in appendix B. We were also to calculate Deff from equation 9, and Dtheory form equation 10.
Results:
The constant rate period was
generally similar for all of our trials. For trial 1 (water with 4 millimeter
beads), the drying rate was squirrely, but it oscillated around a rate of 8.78E-4
grams per second. For trial 2 (water with 500 micron beads), the drying rate
was also initially squirrely, but it eventually stabilized to a rate of .001 grams
per second. Trial 3 (ethanol with 4 millimeter beads) had a constant rate
period that lasted nearly the entirety of the trial. This constant rate period
also slowly decreased through the length of the trial. Trial 4 (ethanol with
500 micron beads), had a very quick constant rate period with squirrelly data.
However, the drying rate did oscillate around 0.0038 grams per second. Trial 5
(ethanol with 1 millimeter beads) and Trial 6 (ethanol with 6 millimeter beads)
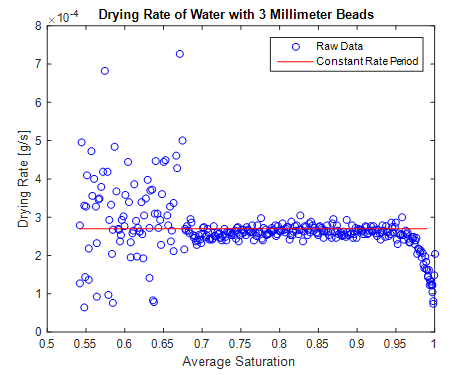
both had a relatively long and stable constant periods. Trial 7 (overnight
water with 3 millimeter beads) initially had a stable constant drying rate, but
it eventually had an oscillating rate.
The second falling rate varied
greatly for each of our trials. The second falling rate was not clear for trial
1. We did not finish this trial, and a second falling rate did seem to be
forming as we approached the end of the trial. However, we did not believe this
drop off in drying rate was conclusive enough, as the drying rate could have
stabilized, and the water sample could have still been in the constant rate
period. The second falling rate was visible for trial 2. This trial showed a
linear fit to the tail end of the mass versus square root of time plot.
Furthermore, the drying rate versus average saturation plot showed a quick and
steady drop off at the end of the trial. The third trial slowly decreased during
the constant rate period, and displayed a miniature second falling rate.
However this was not enough data to analyze. The fourth trial had a second
falling rate which first rose and then fell. The fifth trial had a steadily
decreasing second falling rate. The sixth and seventh trials were not fully
completed, and therefore no second falling rate was observed.
The h values were 26.3±3.4, 34.4±4.5, 23.2±3.0, 48.5±6.3, 38.9±5.1, 20.5±2.7,
and 8.1±1.1 watts per meters squared per degree Kelvin for trials 1 through 7
respectively. The htheory
values were 20.4±.61, 20.9±.62, 19.8±.59, 20.9±.63, 20.8±.62, 19.7±.59, 18.9±.57
watts per meters squared per degree Kelvin for trials 1 through 7 respectively.
The Keff values were .018±8.2E5
and .0436±.009 watts per meters per degree Kelvin for trials 2 and 5
respectively. The Deff
values were .00014±2.6E6 and .000013±3.9E6 centimeters squared per second for trials
2 and 5 respectively. The Dtheory
values were 1.5E-5±9E7 and 9.2E-6±5.5E7 centimeters squared per second for
trials 2 and 5 respectively.
Figure 2: A plot displaying the loss of
mass versus time for ethanol in trial 5. The linear fit of trial 5 for the
constant rate period is shown in red. The fit is close to linear because we
used a large amount of ethanol.
Figure 3: The constant rate curve for
trial 5. The period is close to constant because we used a large amount of
ethanol.
Discussion:
The plots of mass versus time do no display perfectly
linear fits because of error. First off, there was error when measuring the
loss of liquid mass, because the scales could only measure to a tenth of a
gram. Secondly, there was error in the time because the stop watch only
measured to a second. Also, the time measurements were actually estimates
because there was pause between the recording of the measurements of mass and
time. In addition, the constant rate period was estimated by myself, which is a
source of human error. Furthermore, the water plots of mass versus time
(figures 4 and 6) show more linear fits when compared to the ethanol plots
(figures 2,9,11 and 13), because the ethanol trays were removed from the dryer
more often. Therefore, the ethanol samples were cooling for twice as long
outside of dryer when compared to the water samples.
For figures 3, 5, 7, 10, 12, and 14 no perfect constant
rate periods were displayed because of the constraint of having to remove the
trays from the dryer. However, the overnight water tray did display a
semi-constant period when compared to the other trials (figure 16). This
constant rate period was interrupted, because when we began to take
measurements of other tray the next morning, we bumped the tray a large number
of times. This skewed the drying rate of the overnight trial and ruined its
consistency.
The Reynolds number had error in the uinf because the air flow meter only measured to one
hundredth of meters per second, so the percent error was 1 percent. The L measurement because the tape ruler,
because it only measured to a millimeter, so the percent error in length was
negligible.
The
h values have larger values than the theoretical because we were constantly
weighing the tray samples. This caused an influx in disruption, which gave us h
values that were larger than theory. Furthermore, the h values had error in the
temperatures (negligible), area which came from ruler measurements (2 percent
error), and change in mass over time measurements (10 percent error). The htheory had an error of 1
percent from the diameter measurement, 1 percent from the insulation
measurement, and 1 percent from the Reynolds number.
Trials 1 and 3 did not display second falling rates,
instead they display slowly decreasing constant rate periods. This is because
the gaps between the beads were too large, and therefore there was too much
space to inhibit a mass transfer to create a second falling rate. Trials 2 and
5 had small enough beads to inhibit mass transfer, and display a second falling
rate.
The Deff
and Keff
values were calculated from an array of values that occurred over the span
of the second falling rate. This was then averaged and the standard deviation
was taken to be the error. The discrepancy between Deff and Dtheory
comes from several variables containing uncertainties in equations 8 and 9. The
concentration of gas, height of liquid, porosity, dm/dt, partial pressures,
area, Schmidt number, Prandtl number, and temperatures all contain
uncertainties. Furthermore, the Deff
values were much lower because the beads were not packed down, and the gas was
constantly being disrupted when the trays were weighed. The discrepancies
between Keff and Ktheory come from many of
the same uncertainties such as dm/dt, area, temperature, and height of liquid
level.
The error in Dtheory
came from assuming the error in the porosity was six percent, because porosity
is defined by two volume measurements, which is six length measurements. This
is shown in appendix C
Conclusion:
The
values of h and Deff were large when compared to theory, because we were
constantly disrupting the samples by measuring the masses. This would not be a
problem if the dryer could measure the masses of multiple samples at the same
time.
We
were able to obtain constant rate periods for all of the trials because the
constant rate period only depends on external forces of heating. However, we
were not able to obtain second falling rates for all of the trials because we
used beads which were too large. If we want more accurate data of the second
falling rate we need to invest in a new dryer which can weigh multiple trays
over time. We also need to even more trials with even smaller beads.
In
the future, we shall invest in smaller beads up to 1 micron in diameter. This
will allow us to analyze the second falling rate more accurately. Furthermore,
with beads in 1 micron in size, we will also be able to analyze and examine the
first falling rate.
Nomenclature
Table:
Table 2: Trial 7 Data A
References:
1.
Tseregounis,
S., Powell, R., 2016, Drying Porous Media, ECH 155, University of California,
Davis.
2.
Bird,
R., Stewart, W., Lightfoot, E., 1960, Transport
Phenomena, John Wiley & Sons Inc. New York.
3.
Whitaker,
S., 1981, Fundamental Principles of Heat Transfer, R.E. Krieger Publishing
Company, Malabar, Florida
4.
Pharmaceutical Dryers, Pharmacetuctical Machinery, Retrieved
February 2, 2016 from http://www.pharmaceuticalmachinery.in/pharmaceutical_dryer.htm
5.
Freeze Dry Applications, Cuddon Freeze Dry, “ISO 9001 Bureau
Veritas Certification”, Retrieved February 3, 2016 from http://www.cuddonfreezedry.com/applications/
6.
Carranza, J., Heat and Mass Transfer in Drying, Retrieved February 1, 2016 from http://ww.chemicalonline.com/doc/drying-technologies-in-the-chemical-industry0002#liquid
Appendix
A: Raw
Data
Figure 4: A plot displaying the loss of mass versus
time for water in trial 1. The linear fit of trial 1 for the constant rate
period is shown in red. The fit is close to linear because we used a large amount
of water.
Figure 5: The constant rate curve for
trial 1. The period is close to constant because we used a large amount of
water.
Figure 6: A plot displaying the loss of mass versus
time for water in trial 2. The linear fit of trial 2 for the constant rate
period is shown in red. The fit is decently close to linear because we used a
decent amount of water.
Figure 7: The constant rate curve for
trial 2. The period is close to constant because we used a large amount of
water.
Figure 8: A plot of the loss of mass versus square
root of time during the second falling rate for trial 2. The second falling
rate is the linear fit in red.
Figure 9: A plot displaying the loss of mass versus
time for ethanol in trial 3. The linear fit of trial 3 for the constant rate
period is shown in red.
Figure 10: The constant rate curve for
trial 3.
Figure 11: A plot displaying the loss of mass versus
time for ethanol in trial 4. The linear fit of trial 4 for the constant rate
period is shown in red.
Figure 12: The constant rate curve for
trial 4. The period is close to constant because we used a large amount of
ethanol.
Figure 13: A plot displaying the loss of mass versus
time for ethanol in trial 6. The linear fit of trial 6 for the constant rate
period is shown in red. The fit is close to linear because we used a large
amount of ethanol.
Figure 14: The constant rate curve for
trial 6. The period is close to constant because we used a large amount of
ethanol.
Figure 15: A plot displaying the loss of mass versus
time for water in trial 7. The linear fit of trial 7 for the constant rate
period is shown in red. The fit is close to linear because we used a large
amount of water.
Figure 16: The constant rate curve for
trial 7. The period is close to constant because we used a large amount of
water. This was interrupted when we started bumping the tray.
Table 1: Overall Data
Side Length (m)
|
U(inf) [m/s]
|
Kine. visco at 70 deg F [m2/s]
|
NRe
|
0.277
|
0.9
|
1.52E-05
|
16362.46
|
Temperature
|
|||
Time (min)
|
Dry Air (C)
|
Wet Bulb (C)
|
|
0
|
49
|
36
|
|
61
|
48
|
37
|
|
123
|
48.5
|
37
|
|
176
|
49
|
37.5
|
|
283
|
50
|
39
|
|
340
|
49.5
|
38
|
|
367
|
51
|
40
|
|
406
|
50
|
40
|
Table 2: Trial 7 Data A
Tray diameter [cm]
|
Tray height [cm]
|
Water/bead height [cm]
|
11.246
|
7.845
|
1.31
|
Mass of Tray
|
Mass of Tray+Beads
|
Total Mass
|
(g)
|
(g)
|
(g)
|
163.3
|
344.1
|
400.1
|
Table 3: Trial 7 Data B
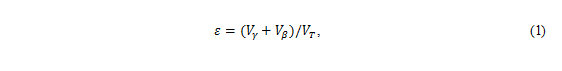
























Comments
Post a Comment