Mass Transfer in Packed Beds
By:
Brett Koehn
Submitted June 5, 2015
Based on experimental work for Laboratory #7,
conducted between May 14, 2015 and March 28, 2015 with group
members
Gary Banh and E.J. Crowley
in Section 5 of ECH 145B
Table
of Contents:
Abstract………………………………………………………………………………………………………………………………………………..3
Introduction…………………………………………………………………………………………………………………………………………....3
Theory…………………………………………………………………………………………………………………………………………………5
Experimental Methods………………………………………………………………………………………………………………………………...7
-Figure
1…………………………………………………………………………………………………………………………………...8
-Figure
2…...………………………………………………………………………………………………………………………………9
Results………………………………………………………………………………………………………………………………………………..11
-Figure
3………………………………………………………………………………………………………………………………….11
-Figure
4………………………………………………………………………………………………………………………………….12
-Figure
5……………………………………………………………………………………………………………………………….…13
-Figure
6……………………………………………………………………………………………………………………….…………14
Discussion……………………………………………………………………………………………………………………………………………15
Design………………………………………………………………………………………………………………………………………………..17
Table
1………………………………………………………………………………………………………………………………...…17
Figure
7…………………………………………………………………………………………………………………………………..18
Conclusion………………………………………………………………………………………………………………………………………...…19
Nomenclature
Table…………………………………………………………………………….……………………………………………………19
-Table
2…………………………………………………………………………………………………………………………………..19
References……………………………………………………………………………………………………………………………………………20
Appendix A……………………………………………………………………………………………………………………………..……………21
Figure
8……………………………………………………………………………………………………………………………..……21
Figure
9………………………………………………………………………………………………………………………………..…22
Figure
10…………………………………………………………………………………………………………………………………23
Figure
11…………………………………………………………………………………………………………………………………24
Figure
12…………………………………………………………………………………………………………………………………25
Figure
13…………………………………………………………………………………………………………………………………26
Figure
14…………………………………………………………………………………………………………………………………27
Table
3…………………………………………………………………………………………………………………………………...28
Table
4…………………………………………………………………………………………………………………………………...28
Table
5…………………………………………………………………………………………………………………………………...29
Table
6………………………………………………………………………………………………………………………………...…36
Appendix B………………………………………………………………………………………………………………………………………..…38
Figure
15…………………………………………………………………………………………………………………………………38
Figure
16…………………………………………………………………………………………………………………………………39
Appendix C………………………………………………………………………………………………………………………………...………...40
Figure
17…………………………………………………………………………………………………………………………………40
Abstract:
During
this lab, we analyzed synthesis gas or ‘syngas’, which is a fuel that can be created with
methane and oxygen. Methane is a greenhouse gas that accounts for 10% of all
greenhouse gas emissions. Therefore reducing methane emissions is good for the
environment. Converting landfill methane emissions into syngas is a useful
process because it produces fuel, stops methane emissions, and only requires
oxygen. However, this reaction requires a catalyst that does not work in the
presence of water. Therefore to create syngas air must be scrubbed of water
moisture. Another solution is to purchase pure oxygen. We found that column
with a packed bed full of Drierite can be used to remove the water moisture. 5 of
these columns were then used to create a design schematic that would cost $420
a year, without initial costs. Purchasing the oxygen would cost $12.8 million a
year. Therefore we should purify air ourselves.
Introduction:
The concepts of mass transfer are
very powerful and useful. One important concept of mass transfer is scrubbing.
Scrubbing is used to purify or filter a stream of multiple components.
Typically the stream being scrubbed contains a desirable and undesirable
component. This stream is run through a column of a third component that
removes the undesirable component from the stream. However, the scrubbing
component eventually becomes ineffective, and needs to be replaced. Therefore,
if we understand the mass transfer concepts of scrubbing, we can also determine
when the scrubbing component needs to be replaced.
One practical use of scrubbing is
eliminating hazardous materials such as methanol, ethanol, isopropanol,
butanol, and acetone from gaseous streams.[1] These hazardous
materials are also water soluble. Therefore, if these materials are released
into the environment, they will contaminate drinking water. In this specific
scrubbing example, a mixture of water and amphiphilic block copolymer is used
to scrub the gaseous streams entering. However, the scrubber does become
ineffective. Therefore, it is very useful to know when the mixture of water and
amphiphilic block copolymer will become ineffective.
Scrubbers
are also used in the creation of high fructose corn syrup.[2] High
fructose corn syrup must be purified of unwanted proteins before processing.
Therefore, high fructose corn syrup is scrubbed with activated carbons and
ion-exchange resins. The syrup will not process correctly and will taste
poorly, if high fructose corn syrup is not purified of these unwanted proteins.
The process of scrubbing streams to separate different components accounts for
40%-70% of both capital and operating costs in the process industry.[3]
During this lab, we examined the mass transfer
between water vapor and solid grains of calcium sulfate. The calcium sulfate was placed inside a
column or packed bed and an air stream saturated with water vapor was allowed
to flow through the packed bed. The grains of calcium sulfate rapidly scrubbed
the water vapor from inflowing the air stream, because calcium sulfate absorbs
atmospheric moisture rapidly.[4] Therefore, the exiting air stream
was very pure oxygen with almost no water vapor left. Removing water from the
air stream is important because water can make reaction catalysts ineffective.
During this lab report, we wanted to create “syngas” which cannot be created in
the presence of water, but requires oxygen as a reactant. Therefore we analyzed
the system of the packed bed to determine the cheapest method of obtaining pure
oxygen. We found that creating oxygen ourselves is much cheaper.
Theory:
The mass transfer concepts that are
involved in this packed bed experiment are very complicated. However, several assumptions
can be made to make this system easier to understand. First off, if the packed
bed is treated as a single slab we know that the gas stream interacts with a, which is the contact area per unit of
packed volume of column. We also know the driving force across a is kc
which has units of length per time. Furthermore, we know that driving force for
the mass transfer coefficient will be defined by the difference of the mole
fraction of water inside the airstream, xw,
and the mole fraction of water at the surface the slab, xws. xws
is approximated to be equal to the concentration at the surface of the packed
bed, Cws, and the
equilibrium absorption constant, Keq,
which has units inversely proportional to concentration. Dimensionless equations
for the depletion of water versus time from the inflowing air stream, equation
1, and the absorption of water at the surface of the slab, equation 2, can now
be solved for
The Reynolds number is defined by
4-ECH 145B, Resources, hammond_j-chem-edu_1935.pdf’
5-Science Lab Evaporators: Amazon.com: Industrial & Scientific. Accessed June 3, 2015.
6-Accessed June 6, 2015. http://www.amazon.com/AMT-5586-Y6-Engine-Driven-1000gpm/dp/B00JBKOYOI/ref=sr_1_1?s=industrial&ie=UTF8&qid=1433550200&sr=1-1.
7-Gavin, Jake. "Oxygen Element Facts." Chemicool. Accessed June 1, 2015.
where X
is the normalized water vapor mole fraction in the air stream is the intial mole fraction of water in the
air stream, Y is the normalized water
vapor mole fraction on the surface of the slab, τ is the dimensionless time, t is the time, seconds, NA is the flux of air coming
in, moles per seconds, ε is the
porosity, C is the total molar
concentration of the air stream, moles per cubic meter,, ξ is the dimensionless length within the slab, z is the length traveled in the slab, meters, and L is the total length of the slab,
meters.
These two equations can be solved
with a finite difference approximation to find the best solution for β. This was done by creating a running
approximate α and β values into a finite difference
scheme. This scheme then gave values for approximated values for X and Y. X was plotted against τ
which gave a clear representation of the break through curve. Y was also plotted against ξ which gave a representation of how
much water was being scrubbed out by Drierite.
The best fitted values of α and β were then used found by evaluating the
solution graphically. β and
α were then used to calculate the Reynolds number and the Sherwood number.The Reynolds number is defined by
where
ρ is density, kilograms per cubic
meters, D is diameter, meters, v is velocity, meters per second, and μ is the kinematic viscosity, Pascal
seconds. The Sherwood number can be assumed to be
where
D is the diffusivity of water vapor,
meters cubed per second, and d is the
diameter of the Drierite grains, meters. There
is also one important relationship which was developed by Gupta and Thodos
between the Sherwood number and the Reynolds numbers which is
where
Sc is Schmidt number.
Experimental
Methods:
This lab was begun by weighing
approximately 5 grams of Calcium Sulfate, which is commercially sold as
Drierite. This Drierite was then placed inside of the slab or packed bed as
shown in figure 2 below. The packed bed was then filled with glass wool at the
entrance and exit of the column. Cooling water was then allowed to flow through
the outer shell of the packed bed to create a counter current heat exchanger.
However, cooling water was only used for half of the trials. Next the wet air
was allowed to flow through the glass wool and Drierite which were both inside the
shell of the packed bed. The Drierite removed the moisture from the wet air,
which allowed dry air to flow out the end of the packed bed. Thermocouples were
then placed on the bottom and top of the packed bed. These thermocouples
measured the temperatures of the dry air coming out and the wet air coming in.
Once the packed bed was set up with wet air flowing through it, we started taking
pictures of the packed bed. We were able to take pictures of the packed bed by
using the automated camera program. The lens of the camera was also position
horizontally in order to make the data analysis easier. Figure 1 shows some
experimental photos that we took at the beginning middle and end of our
experiment.
Figure 1: This
figure above shows the progression of Drierite absorbing water moisture for
Trial 3. The top picture was taken at a time of 40 seconds. The middle picture
was taken at a time of 455 seconds. The third picture was taken at a time of
1025 seconds.
We used flow rates of 12.944 liters
per second, 11218 liters per seconds, 5000 liters per seconds, and 2000 liters
per seconds for trials 1, 2, 3, and 4 respectively. Trials 1 and 4 were
performed without cooling water. Trials 2 and 3 were performed with cooling
water.
Figure 2: This
figure above shows a detailed sketch of the packed bed full of Drierite. Wet
air comes in through the bottom of the column, and dry air comes out the top of
the column. The temperatures at the top and bottom of the column were measured
with thermocouples. Cooling water was also used for half of the trials.
We
then analyzed the pictures of the packed bed by using Matlab. We assumed that
blue and red Drierite corresponded to Y values of 1 and 0 respectively. This allowed us to calculate the Y versus ξ, which was obtained by equation 3d. We
then plotted Y versus ξ for specific
times. We then fit this data numerically by using a finite differences solution
on equations 1 and 2. Finally, we calculated the best fit curves.
ξ was then
calculated for when Y reached values .25 and .75. We then plotted this against τ, which was calculated with equation 3c
and numerically fit this by using a finite differences approach on equations 1
and 2. This approach best fit the data in figures and simultaneously found
values of α
and β. This was done
until the best values of α
and β were found. The temperature of the thermocouples versus
time was calculated and plotted for a cooling and non-cooling trial. The
Reynolds and Sherwood numbers were then calculated with equations 4 and 5
respectively. The Reynolds and Sherwood number was then plotted against the
Reynolds numbers. Theoretical curves were then superimposed over this plot with
data obtained from equation 6.
Results:
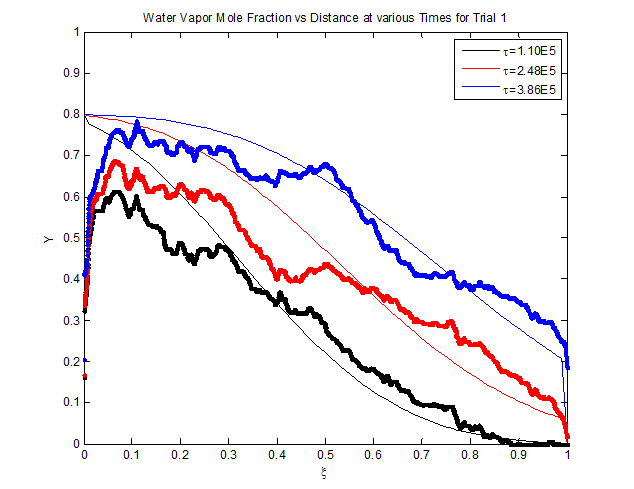
Figure 3: This
figure above shows Y versus ξ. This data was obtained from the
experimental values obtain during trial 1 without cooling.
As
shown figure 3, the variable Y was
plotted versus ξ. These values were
plotted for different τ values. The experimental values of Y decreased as the values of ξ increased for all of the trials that
we analyzed. Furthermore, the numerically fitted data values of Y also decreased as the values of ξ increased. The break through curve is
the section in the best fit lines where the slope initially decreases at an
increasing rate, eventually reached a slope which is completely vertical, and
finally the slope increases at a decreasing rate until the curve is level. This
region of the curve represents the where the Drierite is completely saturated
with water vapors. Therefore, the water moisture is “breaking through” the
packed bed. The experimental data sets also have a break through region. However,
this region is much harder to determine. Therefore, the break through regions
had to be estimated.
Figure 4: This
figure above shows ξ versus τ. This data was obtained from the
experimental values obtain during trial 1 with cooling. The blue data
represents the dimensionless distance for when Y=.25. The red data represents the dimensionless distance for when Y=.75. The error bars are 2 standard
deviations of ξ.
As
shown in figure 4, the variables ξ25
and ξ75 were plotted
against τ. ξ25 and ξ75
were the dimensionless distances when Y
was equal to .25 and .75 respectively. The values of ξ25 increased logarithmically as the experiment preceded
for all of the trials. The values of ξ75
increased exponentially as the experiment preceded for all of the trials. The
experiments had τ values that ranged
from 0 to 3.5E6.
Figure 5: This figure above shows temperature
versus time for trial 1 and trial 2. Trial 1 is the trial without cooling, and
trial 2 was done with cooling.
As
shown in figure 5, the temperatures at the top and bottom of the packed bed
were plotted against dimensional time. The top of the column without cooling had
the highest temperatures, which is represented in figure 5. The temperatures of
the top of the column with cooling water, the bottom of the column with cooling
water, and the bottom of the column without cooling water all had temperatures
of about 24 degrees Celsius throughout the trials. Furthermore,
initially the top of the temperature at the top of the column is less than the
temperature at the bottom of the column for trials 1 and 2. Figure 14 represents
the data from obtained trials 3, which had cooling, and trial 4, which had no
cooling. As shown in figure 14 the temperatures at the bottom of the column
with and without cooling water remain constant at 22 degrees Celsius.
The temperature at top of the column without cooling water was the highest
temperature for the full duration of the trials. The temperature at the bottom
of the column with cooling water was the lowest temperature for the full
duration of the trials.
Figure 6: This
figure above shows the Sherwood number plotted against the Reynolds number. The
error bars are two standard deviations of the Reynolds number and Sherwood
number for horizontal and vertical directions respectively. The experimental
data increases at a logarithmic rate which agrees with the theoretical data.
As
shown in figure 6, the Sherwood number was plotted against the Reynolds number.
These were found from our values of α
and β. α had values of .7±.32, .89±.69,
.80±.56, .20±.17 for trials 1-4. β
had values of 15.3±7.6, 4.21±5.76, 6.5±3.98, and 53±23.4 for trials 1-4. The
values of the Reynolds numbers were 347±3.12, 300±4.62, 133±5.23, and 53.4±2.5
for trials 1-4. The Sherwood numbers were 35.6±29, 33.7±43, 21.9±48.6, and
31.3±23.3.
Discussion:
From figure 3, we know that the
experimental values Y decreases as ξ increases. This is because as water
moisture flows through the Drierite, and the Drierite becomes saturated. Once
the Drierite is saturated, it can no longer absorb water. Therefore as the
dimensionless distance increases in the packed bed, the relative mole fraction
on the surface of the packed bed will eventually be very small compared to the
mole fraction of water flowing in the air stream. The mole fraction in the air
stream will eventually reach zero, and likewise Y eventually reached 0. Therefore, as the time increased during
this experiment, every value of Y became
0. This happened because the packed bed became fully saturated with water after
a certain amount of time has passed during this experiment.
From figure 4, we know that the
experimental values of Y increases as
τ increases. This agrees with figure 3,
because it shows that the packed bed is becoming more saturated with water over
time. Figure 4 also shows that Y approaches 1 at higher values of τ. Furthermore, there are more values of
ξ25 when compared to ξ75. This shows that the mass
transfer decreases with time and distance.
From figure 5, we see that the
reaction between water and Drierite is an exothermic reaction, because the
temperature at the top of the packed bed is much higher without cooling. We
also know that the absorption process takes longer when cooling is not used
because the cooling trials took less time. The mass transfer is more effective
when cooling is used because the Drierite absorbs water the best at low
temperatures. Drierite releases water moisture at high temperatures, which is
bad for the mass transfer between Drierite and water.
The mass transfer coefficient
increases as the flow rate increases. kc
is in units of meters per seconds. Therefore increasing the velocity will
increases the value of kc.
In addition, the mass transfer coefficient will decrease if we were to scale up
this process. As the process gets larger, the value of a get smaller. a gets
smaller because the volume will become much larger compared to the interaction
area.
We used to limiting cases while
performing our experiments. The thing we limited was flow rate. The flow rates
were limited to values of 5 liters per second and 2 liters per second. However,
these flowrate are only valid if the Reynolds number is between 1900 and
10,400. These values are acceptable theoretically. This is represented in
figure 6 as the experimental data agrees with literature values. This is
because the calculated mass transfer coefficients were within the except error
bounds. We also limited our time. The time was limited to 450 seconds.
The error in the mass transfer
coefficient is 2 standard deviations vertically for the Sherwood number and 2
standard deviations for the Reynolds number.
The error bounds for the calculated
mass transfer coefficient α
were .32, .69, .56, and .17 for trials 1-4. β
had error bounds values of 7.6, 5.76, 3.98, 23.4 for trials 1-4. The error in
these results is large because β and α were based on a lot of uncertain
quantities such as the mole fraction of water, length, time, flow rate, and
temperature.
The temperature graph shows us that
this reaction is going to produce a lot of heat if we scale up this backed bed.
Therefore, we need to make sure we have enough cooling water so none of the
equipment is damaged. Furthermore, sufficient cooling is also important for the
reaction to proceed at maximum efficiency because Drierite absorbs more water
at lower temperatures.
Design:
We
need to design a packed bed which can provide enough pure oxygen to react 10
million cubic feet of methane each year and create the valuable fuel, syngas.
This is equal to about 3.3 billion moles of methane. Therefore, we need about
1.65 billion moles of oxygen each year because the reaction requires 1 mole of
oxygen to react with two moles of methane. This is equal to incoming air flow
rate of 14.8 million cubic feet each year or an incoming flow rate of 2.1 cubic
feet per second.
2.1
cubic feet per second is an extremely large incoming flow rate. However, if we
utilize a condenser, such as the industrial evaporator vacuum controller, we
only need an inflow airstream of around 1.35 cubic feet per second.[5]
The engine driven pump that we use meets this flow rate requirement of 1.35
cubic feet per seconds.[6] The flow rate will then enter 4 of the
active columns and eventually react with the methane as pure oxygen. The piping,
tubing, and columns can all be purchased from the same corporation.[7]
The prices of the previously mentioned equipment is shown in table 1.
The
design scheme costs $67,701.11 to produce the required amount of pure oxygen.
However, this price is deceivingly expensive. The initial costs for this design
project are $67,281.11. The annual cost of running this design is only $420 per
year. The annual cost of purchasing oxygen is about $12,800,000. After the
initial year, the design scheme costs approximately 30 thousand times less each
year. Therefore, this scrubber will become more profitable the longer it is
operated.
Figure 7: The
schematic design is shown figure 7. This design requires a pump, a condenser, 5
columns, and a heater. The heater is not shown because the heater is not a part
of the cyclic process this schematic undergoes. There is also cooling water
running counter current through each of the columns.
The design schematic is shown in
figure 7. This design contains 5 columns which will all have cool water running
through them. However, one of these columns is always inactive. The column goes
inactive because there is valve which can be closed below each column.
Therefore, an employee can close the valve below the column. The employee can
then remove the inactive column and extract the saturated Drierite. The
moisture is then removed from the Drierite by a heater. The Drierite is then
placed inside the inactive column. The inactive column is then made active
again by opening the closed valve below the column. The employee will
continuously cycle through each column. Therefore, no wet air is ever allowed
into the reactor.
Conclusion:
We should scrub atmospheric air
ourselves instead of purchasing pure oxygen. Syngas can be created once we have
the pure oxygen and methane from the landfill. Therefore, we can stop methane
emissions from the landfill, and create a valuable fuel. Annual cost of
scrubbing oxygen ourselves is $420. The annual cost of buying pure oxygen is
$12.8 million a year. However, the design will be completely ineffective if
there is not a very efficient condenser and powerful pump. The values we
received for the dimensionless mass transfer coefficients were .7±.32,
.89±.69, .80±.56, .20±.17 for α
and 15.3±7.6,
4.21±5.76, 6.5±3.98, and 53±23.4 for β.
The values we received for the Reynolds number were 347±3.12,
300±4.62, 133±5.23, and 53.4±2.5. The values we
received for the Sherwood number were 35.6±29, 33.7±43,
21.9±48.6, and 31.3±23.3.
Nomenclature Table:
Table
2: Nomenclature Table
References:
1-Jacobs,
John. "Air Pollution Control Technology Fact Sheet." Packed Beds.
2009. Accessed June 4, 2015.
2-Parker,
Ken. Production of Syrup. 2008.
3-Kovel,
Nick. "For Absorption, Desorption, Rectification and Direct Heat
Transfer." In Packed Bed Columns. Vol. 1. Elsevier, 2006.4-ECH 145B, Resources, hammond_j-chem-edu_1935.pdf’
5-Science Lab Evaporators: Amazon.com: Industrial & Scientific. Accessed June 3, 2015.
6-Accessed June 6, 2015. http://www.amazon.com/AMT-5586-Y6-Engine-Driven-1000gpm/dp/B00JBKOYOI/ref=sr_1_1?s=industrial&ie=UTF8&qid=1433550200&sr=1-1.
7-Gavin, Jake. "Oxygen Element Facts." Chemicool. Accessed June 1, 2015.
Appendix A:
Figure 8: This
figure above shows Y versus ξ. This data was obtained from the
experimental values obtain during trial 2 with cooling.
Figure 9: This
figure above shows ξ versus τ. This data was obtained from the
experimental values obtain during trial 2 with cooling. The blue data
represents the dimensionless distance for when Y=.25. The red data represents the dimensionless distance for when Y=.75. The error bars are 2 standard
deviations of ξ.
Figure 10: This
figure above shows Y versus ξ. This data was obtained from the
experimental values obtain during trial 3 with cooling.
Figure 11: This
figure above shows ξ versus τ. This data was obtained from the
experimental values obtain during trial 3 with cooling. The blue data
represents the dimensionless distance for when Y=.25. The red data represents the dimensionless distance for when Y=.75. The error bars are 2 standard
deviations of ξ.
Figure 12: This
figure above shows Y versus ξ. This data was obtained from the
experimental values obtain during trial 4 without cooling.
Figure 13: This
figure above shows ξ versus τ. This data was obtained from the
experimental values obtain during trial 4 without cooling. The blue data
represents the dimensionless distance for when Y=.25. The red data represents the dimensionless distance for when Y=.75. The error bars are 2 standard
deviations of ξ.
Figure 14: This
figure above shows temperature versus time for trial 3 and trial 4. Trial 3 is
the trial with cooling, and trial 4 was done without cooling.
Table 3: Trial 1
Raw Data
Photo
|
Temp C Top
|
Bottom
|
Flow Rate
|
reading
|
mL
|
mass (g)
|
1
|
22
|
25
|
steel
|
100
|
12944
|
10.633
|
2
|
24
|
24
|
||||
3
|
33
|
25
|
||||
4
|
38
|
25
|
||||
5
|
40
|
24
|
||||
6
|
43
|
24
|
||||
7
|
43
|
25
|
||||
8
|
42
|
24
|
||||
9
|
41
|
24
|
||||
10
|
40
|
24
|
||||
11
|
39
|
24
|
||||
12
|
37
|
24
|
||||
13
|
36
|
24
|
||||
14
|
35
|
24
|
||||
15
|
34
|
24
|
||||
16
|
33
|
24
|
Table 4: Trial 2
Raw Data
Photo
|
Temp C Top
|
Bottom
|
Flow Rate
|
reading
|
mL
|
mass (g)
|
1
|
17
|
25
|
steel
|
95
|
11218
|
12.537
|
2
|
17
|
25
|
||||
3
|
25
|
25
|
||||
4
|
28
|
24
|
||||
5
|
28
|
24
|
||||
6
|
28
|
24
|
||||
7
|
27
|
24
|
||||
8
|
26
|
24
|
||||
9
|
25
|
24
|
||||
10
|
24
|
24
|
||||
11
|
24
|
24
|
||||
12
|
23
|
24
|
||||
13
|
23
|
24
|
||||
14
|
23
|
24
|
||||
15
|
22
|
24
|
Table 5: Trial 3
Raw Data
Photo
|
Temp C Top
|
Bottom
|
Flow Rate
|
reading
|
mL
|
mass (g)
|
1
|
22
|
23
|
glass
|
20
|
961
|
5.137
|
2
|
22
|
22
|
steel
|
40
|
4732
|
|
3
|
22
|
22
|
||||
4
|
20
|
22
|
||||
5
|
20
|
22
|
||||
6
|
19
|
22
|
||||
7
|
19
|
20
|
||||
8
|
19
|
22
|
||||
9
|
19
|
22
|
||||
10
|
19
|
22
|
||||
11
|
19
|
22
|
||||
12
|
19
|
22
|
||||
13
|
19
|
22
|
||||
14
|
19
|
22
|
||||
15
|
19
|
22
|
||||
16
|
19
|
22
|
||||
17
|
19
|
22
|
||||
18
|
19
|
22
|
||||
19
|
19
|
22
|
||||
20
|
19
|
22
|
||||
21
|
19
|
22
|
||||
22
|
19
|
22
|
||||
23
|
19
|
22
|
||||
24
|
19
|
22
|
||||
25
|
19
|
22
|
||||
26
|
19
|
22
|
||||
27
|
19
|
22
|
||||
28
|
19
|
22
|
||||
29
|
19
|
22
|
||||
30
|
19
|
22
|
||||
31
|
19
|
22
|
||||
32
|
19
|
22
|
||||
33
|
19
|
22
|
||||
34
|
19
|
22
|
||||
35
|
19
|
22
|
||||
36
|
19
|
22
|
||||
37
|
19
|
22
|
||||
38
|
19
|
22
|
||||
39
|
19
|
22
|
||||
40
|
19
|
22
|
||||
41
|
19
|
22
|
||||
42
|
19
|
22
|
||||
43
|
19
|
22
|
||||
44
|
19
|
22
|
||||
45
|
19
|
22
|
||||
46
|
19
|
22
|
||||
47
|
19
|
22
|
||||
48
|
19
|
22
|
||||
49
|
19
|
22
|
||||
50
|
19
|
22
|
||||
51
|
19
|
22
|
||||
52
|
19
|
22
|
||||
53
|
19
|
22
|
||||
54
|
19
|
22
|
||||
55
|
19
|
22
|
||||
56
|
19
|
22
|
||||
57
|
19
|
22
|
||||
58
|
19
|
22
|
||||
59
|
19
|
22
|
||||
60
|
19
|
22
|
||||
61
|
19
|
22
|
||||
62
|
19
|
22
|
||||
63
|
19
|
22
|
||||
64
|
19
|
22
|
||||
65
|
19
|
22
|
||||
66
|
19
|
22
|
||||
67
|
20
|
22
|
||||
68
|
20
|
22
|
||||
69
|
20
|
22
|
||||
70
|
20
|
22
|
||||
71
|
20
|
22
|
||||
72
|
20
|
22
|
||||
73
|
20
|
22
|
||||
74
|
20
|
22
|
||||
75
|
19
|
22
|
||||
76
|
20
|
22
|
||||
77
|
20
|
22
|
||||
78
|
20
|
22
|
||||
79
|
20
|
22
|
||||
80
|
20
|
22
|
||||
81
|
20
|
22
|
||||
82
|
20
|
22
|
||||
83
|
20
|
22
|
||||
84
|
20
|
22
|
||||
85
|
20
|
22
|
||||
86
|
20
|
22
|
||||
87
|
20
|
22
|
||||
88
|
20
|
22
|
||||
89
|
20
|
22
|
||||
90
|
20
|
22
|
||||
91
|
20
|
22
|
||||
92
|
20
|
22
|
||||
93
|
20
|
22
|
||||
94
|
20
|
22
|
||||
95
|
20
|
22
|
||||
96
|
20
|
22
|
||||
97
|
20
|
22
|
||||
98
|
20
|
22
|
||||
99
|
20
|
22
|
||||
100
|
20
|
22
|
||||
101
|
20
|
22
|
||||
102
|
20
|
22
|
||||
103
|
20
|
22
|
||||
104
|
20
|
22
|
||||
105
|
20
|
22
|
||||
106
|
20
|
22
|
||||
107
|
20
|
22
|
||||
108
|
20
|
22
|
||||
109
|
21
|
22
|
||||
110
|
21
|
22
|
||||
111
|
21
|
22
|
||||
112
|
21
|
22
|
||||
113
|
21
|
22
|
||||
114
|
21
|
22
|
||||
115
|
21
|
22
|
||||
116
|
21
|
22
|
||||
117
|
21
|
22
|
||||
118
|
21
|
22
|
||||
119
|
21
|
22
|
||||
120
|
21
|
22
|
||||
121
|
21
|
22
|
||||
122
|
21
|
22
|
||||
123
|
21
|
22
|
||||
124
|
21
|
22
|
||||
125
|
21
|
22
|
||||
126
|
21
|
22
|
||||
127
|
21
|
22
|
||||
128
|
21
|
22
|
||||
129
|
21
|
22
|
||||
130
|
21
|
22
|
||||
131
|
21
|
22
|
||||
132
|
21
|
22
|
||||
133
|
21
|
22
|
||||
134
|
21
|
22
|
||||
135
|
21
|
22
|
||||
136
|
21
|
22
|
||||
137
|
21
|
22
|
||||
138
|
21
|
22
|
||||
139
|
21
|
22
|
||||
140
|
21
|
22
|
||||
141
|
21
|
22
|
||||
142
|
21
|
22
|
||||
143
|
21
|
22
|
||||
144
|
21
|
22
|
||||
145
|
21
|
22
|
||||
146
|
21
|
22
|
||||
147
|
21
|
22
|
||||
148
|
21
|
22
|
||||
149
|
21
|
22
|
||||
150
|
21
|
22
|
||||
151
|
21
|
22
|
||||
152
|
21
|
22
|
||||
153
|
21
|
22
|
||||
154
|
21
|
22
|
||||
155
|
21
|
22
|
||||
156
|
21
|
22
|
||||
157
|
21
|
22
|
||||
158
|
21
|
22
|
||||
159
|
21
|
22
|
||||
160
|
21
|
22
|
||||
161
|
21
|
22
|
||||
162
|
21
|
22
|
||||
163
|
21
|
22
|
||||
164
|
21
|
22
|
||||
165
|
21
|
22
|
||||
166
|
21
|
22
|
||||
167
|
21
|
22
|
||||
168
|
21
|
22
|
||||
169
|
21
|
22
|
||||
170
|
21
|
22
|
||||
171
|
21
|
22
|
||||
172
|
21
|
22
|
||||
173
|
21
|
22
|
||||
174
|
21
|
22
|
||||
175
|
21
|
22
|
||||
176
|
21
|
22
|
||||
177
|
21
|
22
|
||||
178
|
21
|
22
|
||||
179
|
21
|
22
|
||||
180
|
21
|
22
|
||||
181
|
21
|
22
|
||||
182
|
21
|
22
|
||||
183
|
21
|
22
|
||||
184
|
21
|
22
|
||||
185
|
21
|
22
|
||||
186
|
21
|
22
|
||||
187
|
21
|
22
|
||||
188
|
21
|
22
|
||||
189
|
21
|
22
|
||||
190
|
21
|
22
|
||||
191
|
21
|
22
|
||||
192
|
21
|
22
|
||||
193
|
21
|
22
|
||||
194
|
21
|
22
|
||||
195
|
21
|
22
|
||||
196
|
21
|
22
|
||||
197
|
21
|
22
|
||||
198
|
21
|
22
|
||||
199
|
21
|
22
|
||||
200
|
21
|
22
|
||||
201
|
21
|
22
|
||||
202
|
21
|
22
|
||||
203
|
21
|
22
|
||||
204
|
21
|
22
|
||||
205
|
21
|
22
|
||||
206
|
21
|
22
|
||||
207
|
21
|
22
|
||||
208
|
21
|
22
|
||||
209
|
21
|
22
|
||||
210
|
21
|
22
|
||||
211
|
21
|
22
|
||||
212
|
21
|
22
|
Table 6: Trial 4
Raw Data
mass of Drierite
|
Iteration
|
Temp Lower ©
|
Temp Upper ©
|
7.157
|
1
|
22
|
27
|
2.0 L/min
|
2
|
22
|
27
|
3
|
22
|
27
|
|
4
|
22
|
27
|
|
5
|
22
|
27
|
|
6
|
22
|
27
|
|
7
|
22
|
27
|
|
8
|
22
|
27
|
|
9
|
22
|
28
|
|
10
|
22
|
28
|
|
11
|
22
|
29
|
|
12
|
22
|
30
|
|
13
|
22
|
30
|
|
14
|
22
|
31
|
|
15
|
22
|
32
|
|
16
|
22
|
32
|
|
17
|
22
|
33
|
|
18
|
22
|
33
|
|
19
|
22
|
33
|
|
20
|
22
|
34
|
|
21
|
22
|
34
|
|
22
|
22
|
34
|
|
23
|
22
|
34
|
|
24
|
22
|
35
|
|
25
|
22
|
35
|
|
26
|
22
|
35
|
|
27
|
22
|
35
|
|
28
|
22
|
34
|
|
29
|
22
|
34
|
|
30
|
22
|
34
|
|
31
|
22
|
34
|
|
32
|
22
|
34
|
|
33
|
22
|
34
|
|
34
|
22
|
33
|
|
35
|
22
|
33
|
|
36
|
22
|
33
|
|
37
|
22
|
32
|
|
38
|
22
|
32
|
|
39
|
22
|
32
|
|
40
|
22
|
31
|
|
41
|
22
|
31
|
|
42
|
22
|
31
|
|
43
|
22
|
31
|
|
44
|
22
|
30
|
|
45
|
22
|
30
|
|
46
|
22
|
30
|
|
47
|
22
|
30
|



















Comments
Post a Comment